5.1 Defining the Root Finding Prblem with Multiple Variables

What do we want to solve for if we say that we want to find the root of a function with multiple variables? In the lecture we learned that if we solve an equation with two unkown variables like:

\[ f_1(x,y) = c_1, \]

we get a 1-D curve in a 2-D space. We can also call this equation a constraint. One example of this are contour plots. We can plot a function with two variables in a 3-D plot. Therefore we estimate a value \(z\) for the values \(x\) and \(y\) with \(z=f(x,y)\). In a contour plot we plot a contour line for a specific value of \(z\) (or in the equation from above for \(c_1\)).

Let’s look at an example of a contour plot for the function \(f(x,y) = 0.5*sin(x) + cos(y)\):

import Pkg
Pkg.instantiate()

using GLMakie

function contourplot(x, y, z)
    GLMakie.activate!()
    Makie.inline!(true)
    with_theme(theme_dark()) do
        fig =  Figure(resolution = (1200,800))
        axs = [Axis3(fig[1,i]; aspect = :data) for i in 1:2]
        surface!(axs[1], x, y, z; colormap=:viridis, colorrange=(minimum(z), maximum(z)),
            transparency=false)
        contour!(axs[1], x, y, z; levels=20, colormap=:viridis, linewidth=2,
            colorrange=(minimum(z), maximum(z)), transformation=(:xy, minimum(z)),
            transparency=true)
        contour3d!(axs[2], x, y, z; levels = 20, transparency = true)
        hidedecorations!.(axs; grid = false)
        display(fig)
    end
end

contourplot (generic function with 1 method)

# let's define a function
f(x,y) = 0.5*sin(x) + cos(y)
x = LinRange(-2π, 2π, 1000)
y = LinRange(-2π, 2π, 1000)
z = [f(x[i], y[j]) for i in eachindex(x), j in eachindex(y)]

# and plot it
contourplot(x, y, z)

GLMakie.Screen(...)

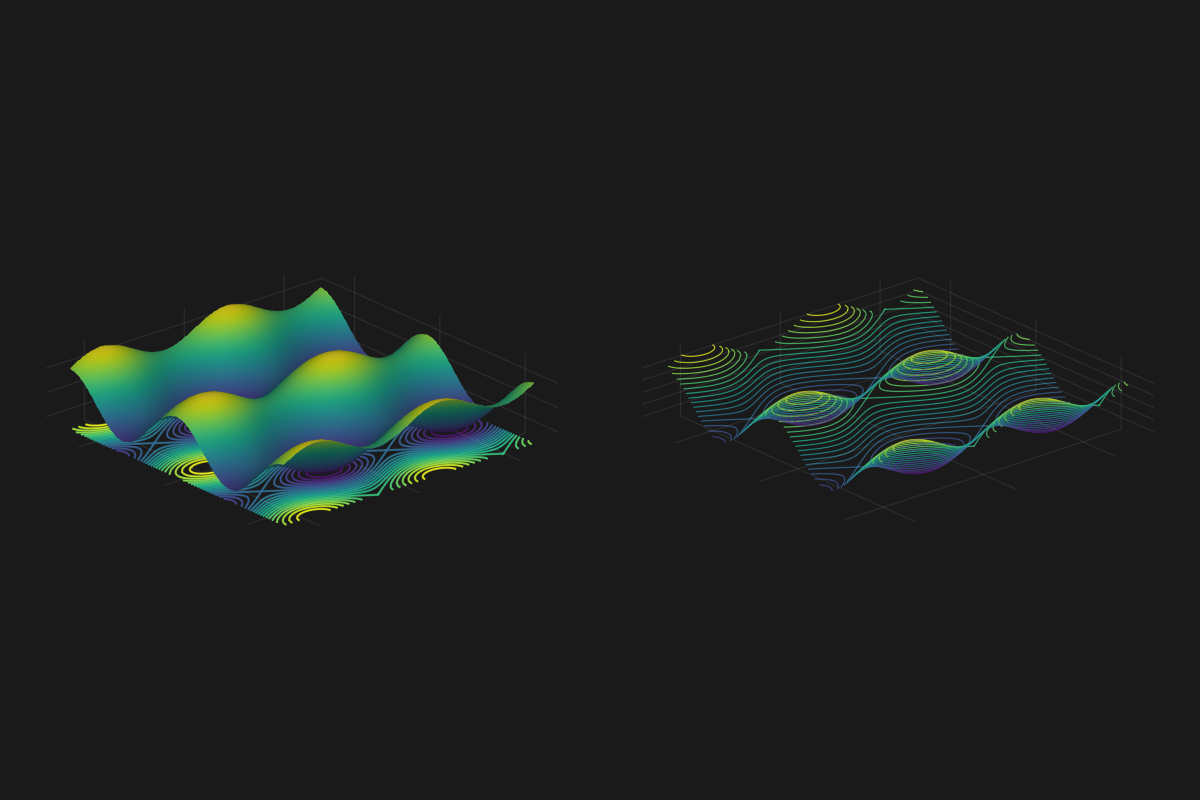
The surfaceplot on the left shows the function \(f(x,y) = 0.5*sin(x) + cos(y)\) in a 3-D plot with a contourplot in the x,y-plane. On the right is a 3-D contourplot. Each color in the contourplot on the right represents a different value of \(z= f(x,y) = 0.5*sin(x) + cos(y)\). So we can interpret it as as a visulaization of where the function \(f(x,y) = 0.5*sin(x) + cos(y)\) is equal to a specific value like \(f(x,y) = 0.5\).

If we add another constraint like:

\[ f_2(x,y) = c_2, \]

we have two constraints. We get two 1-D curves in a 2-D space. The intersection of these two curves is the solution to the equation (a 0-D result). This point is the solution to the equation system. In general: Each independant equation reduces the dimension of the solution space by one.

For example, if we solve the equation system:

\[ f_1(x,y) = 0.5*sin(x) + cos(y) = c_1 = 0, \]

\[ f_2(x,y) = x = c_2 = 0, \]

we get the point (or points - since we can also have multiple solutions), where the two curves of each solution intersect. Here we get all points where \(x=0\) and \(0.5*sin(0) + cos(y) = 0\). One solution therefore ist \(x=0, y=\frac{\pi}{2}, z=0\).

We can rewrite this system of equations into a vector form and make it more general:

The Root Finding Problem

We want to find a vector \(\mathbf{x} = (x_1, \dots, x_n)\), given on a continuous vector-valued function \(\mathbf{f}= (f_1, \dots f_n)\) mapping from \(\mathbb{R}^n\) into \(\mathbb{R}^n\), such that

\[\begin{split} \begin{split}\begin{split} f_1(x_1,\dots,x_n) &= 0,\\ f_2(x_1,\dots,x_n) &= 0,\\ &\vdots\\ f_n(x_1,\dots,x_n) &= 0. \end{split}\end{split} \end{split}\]

We can also write this in a more compact form:

\[ \mathbf{f}(\mathbf{x}) = \mathbf{0}. \]

The solution \(\mathbf{x}\) is called the root of the vector-valued function. How can we find the root of a function with multiple variables?